Viele Anwendungen besitzen eine Farbkorrektur-Möglichkeit mit Gradationskurven. Allerdings wissen die wenigsten User, wie vielfältig sich diese einsetzen lassen...
Bereits die Eindeutschung zeigt sich flexibel, denn es existieren im Deutschen zwei ähnliche Bezeichnungen für den gleichen Sachverhalt: Graduationkurven (mit u!) und Gradationkurven (ohne u!). Aufgrund der Google-Trefferanzahl (776 zu 33.100) spricht die basisdemokratische Mehrheit für den U-Verlust, weshalb wir uns nicht dagegen auflehnen, obwohl unsere Redaktion (aber auch u.a. Adobe) in der Vergangenheit dem U sehr freundlich gesinnt waren.
Für diesen Artikel haben wir die Gradationskurven aus Blender verwendet, da dieses Programm kostenlos erhältlich ist und somit unsere Ausführungen wirklich für Jedermann nachvollziehbar sind. Jedoch findet man die gleiche Funktionalität auch in vielen anderen (kommerziellen) Software-Paketen. Oft tragen sie dabei nur den simplen Namen Curves/Kurven.
Wie geht’s?
Um die Funktionsweise von Gradationskurven zu verstehen, ist eigentlich nur etwas grundsätzliches Verständnis von mathematischen Funktionen und natürlich von Computer-Farbenlehre notwendig. Doch keine Angst. Es ist eigentlich ziemlich durchschaubar...
Bei den Graduationskurven handelt es sich um Funktionen, die beschreiben, wie Eingangswerte (Input-Pixel) in Ausgangswerte (Output-Pixel) umgewandelt werden sollen.
Hierfür werden auf der X-Achse (also die Waagrechte entlang) ein Farb- oder Helligkeitswerte eines Pixels aufgetragen und dann in die Output-Werte auf der senkrechten Y-Achse durch eine entsprechende Funktion transformiert. Nicht klar? Dann mal gleich ein Beispiel.
Nehmen wir einmal einen Pixel aus einem Bild mit einem Helligkeitswert von 128. Wenn wir die Gradationskurve nicht berühren, ist sie eine einfache lineare Funktion, die im 45-Grad Winkel verläuft und einfach durch die Formel f(x) = x, oder für unseren Fall noch einfacher y = x beschrieben wird.
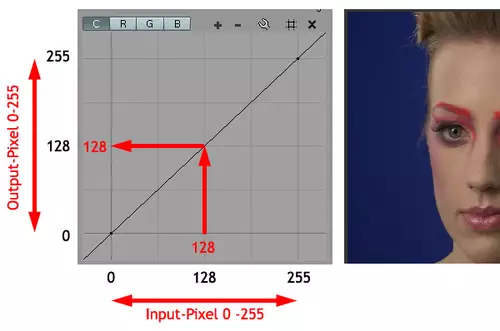
Für jeden Punkt auf der Y-Achse gilt y = x. Unter anderem wird somit auch in unserem Beispiel die Eingangs-Helligkeit von 128 auch auf den Ausgabewert 128 abgebildet. Oder Im Klartext: Es ändert sich nichts bei der Bildausgabe, weil alle Pixel 1:1 abgebildet werden.
Was geht?
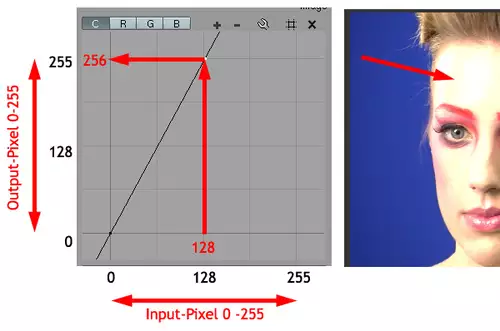
Doch sobald man die Kurve verändert, ändert sich die Ausgabe natürlich entsprechend. Im folgenden Fall lassen wir die Helligkeitskurve doppelt so steil ansteigen. Mathematisch beschreibt man dies mit y = 2x. Wie man sehen kann, wirkt sich dies in einer Helligkeitsveränderung des Bildes deutlich aus. Das Bild wird heller. Alle Input-Pixel über 127 werden jedoch schon in einem Bereich über 255 abgebildet, und sind damit reines Weiß. Das Bild überstrahlt in diesen Bereichen und hat dort keine Zeichnung mehr.
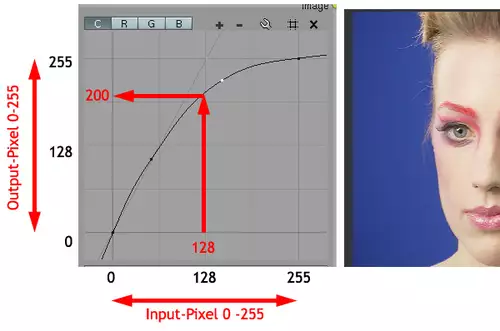
Dies ist ein übliches Problem der linearen Farbkorrektur. Dennoch arbeiten viele einfachen Farbkorrekturen nach diesem System. Bei Gradationskurven sind wir jedoch nicht auf lineare Transformation festgelegt. Wenn wir die Kurve bei dunklen Pixeln nach wie vor stark ansteigen lassen, sie bei bereits hellen Pixeln jedoch stark abflachen, wird das Bild insgesamt ebenfalls heller. Allerdings behält es noch Zeichnung in den hellen Bereichen, da es nach wie vor unterschiedliche Helligkeitsabstufungen gibt (wenn auch nicht mehr so viele)...
Sättigung
Dass man mit der Helligkeitskurve irgendwie die Helligkeit verändern kann, dürfte manchem Leser auch schon vorher klar gewesen sein. Doch auch die Sättigung eines Bildes lässt sich einfach regeln. Die Idee dahinter: Wir komprimieren sozusagen den Bereich der Eingangspixel und strecken diesen auf den den gesamten Bereich der Output-Pixel. Linear würde eine Sättigungsfunktion z.B. so aussehen:
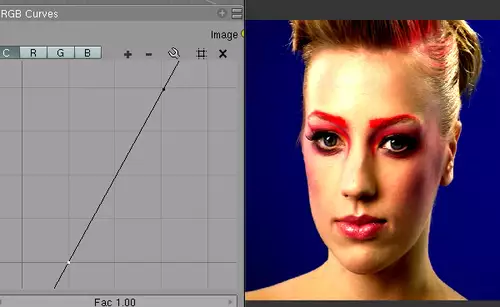
Je steiler die Kurve, desto extremer die Sättigung. Allerdings gehen hierbei schnell die Farbabstufungen aus und es kommt zu flächigen Farben. Wir können uns aber wieder des vorherigen Tricks bedienen und sowohl die dunklen als auch die hellen Pixel sanft abflachen lassen. Der Kontrast-Effekt wirkt dadurch deutlich natürlicher, weil rechnerisch nicht so viele Farbabstufungen durch die Quasi-Quantisierung verloren gehen:
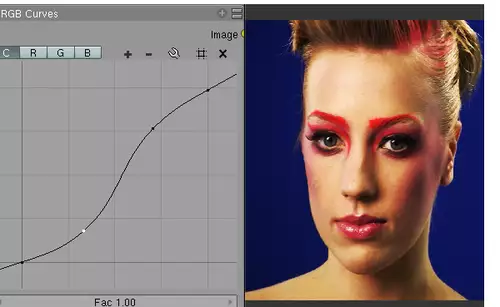
Doch linear muss nicht immer nur schlechter sein. So kann man mit der folgenden Funktion Bereiche gezielt ins Schwarz „absaufen“ lassen, was eine Kontrastveränderung plus Low-Key-Effekt ergibt. So etwas bekommt man mit einem normalen, linearen Kontrast-Regler natürlich nicht hin...
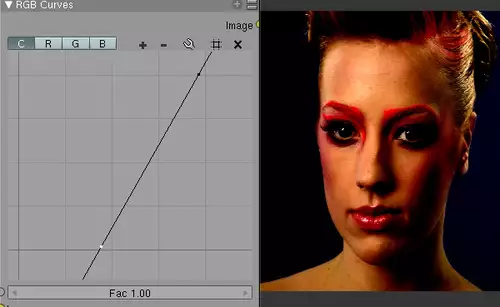
Natürlich bieten sich Gradationskurven auch an, um eine echte Gamma-Korrektur erzeugen. Wenn Bezier-Formen unterstützt werden, ist die typische Verlaufsform schnell eingestellt:
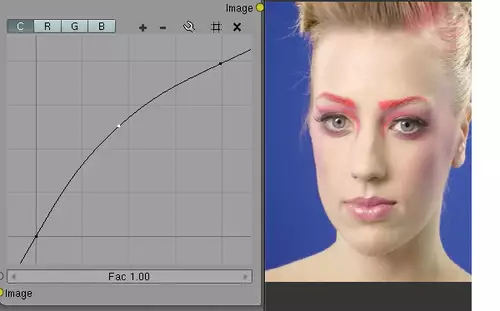
Jetzt wird bunt...
Man kann mit den Kurven aber nicht nur die Helligkeit eines Pixels verändern. Vielmehr lassen sich meistens auch einzelne Farbkanäle separat über Kurven transformieren. Oft werden hierfür die RGB-Kanäle angeboten, jedoch sind auch YUV-Kanäle nicht unüblich.
Beispielsweise lassen sich ausschließlich die Rot-Werte eines Bildes betonen, indem man nur die Rot-Kurve steiler verlaufen lässt....
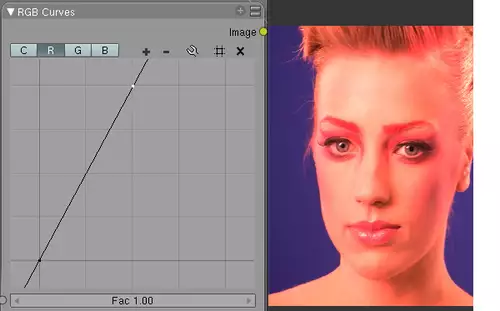
Zugegeben ein seltener Anwendungsfall. Ein praxisnäheres Anwendungsbeispiel für die verschiedenen Farbkurven könnte z.b. die Korrektur eines Farbstichs sein. Das folgende Bild haben wir absichtlich in der Sonne mit dem Weißabgleich für Kunstlicht aufgenommen. Wenn wir mit der Maus in das Bild an eine Stelle klicken, die eigentlich weiß sein sollte, erhalten wir folgende Werte: R = 100, G = 165, B = 247.
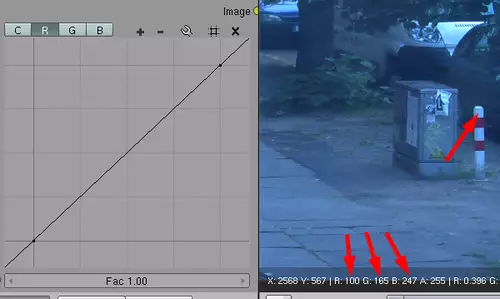
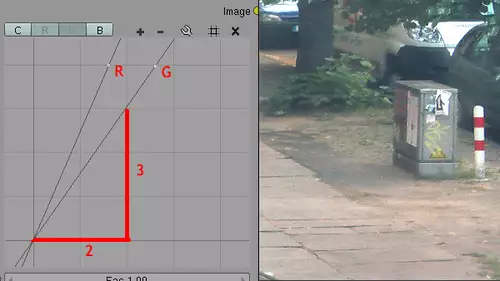
Für ein richtig belichtetes Weiß sollten die Werte jedoch ungefähr gleich sein, also R = 247, G= 247, B= 247. Um dies zu erreichen, muss also der Rot-Wert von 100 auf 247 gebracht werden, was einer Steigung von 247/100 oder ca. 2,5 entspricht. Die korrigierende Grünkurve sollte nach dieser Logik eine Steigung von 247/165 aufweisen, was ziemlich genau 1,5 entspricht.
Achtung, angewandte Schulmathematik: Bei der Einstellung der Kurven können die eingeblendeten Quadrate sehr hilfreich sein. Um zum Beispiel die Steigung der Grünkurve einzustellen, bringen wir den Bruch auf den kleinsten, ganzzahligen Nenner: 1,5 = 3/2. Nun können wir die Steigung an dem Quadraten abzählen und gehen 2 Quadrate nach rechts und 3 Quadrate nach oben. Bei Rot gehen wir 2 nach rechts und 5 nach oben. Wenn wir nun die Kurven mit der entsprechenden Steigung einstellen...
...Voilà. Der falsche Weißabgleich ist korrigiert.
Selektive Wahrnehmung
Wer normalerweise mit einer 3-Wege-Farbkorrektur arbeitet, kann viele Operationen ebenfalls mit Gradationskurven simulieren. Sogar mit mehr Freiheiten, denn die Bereiche für Schatten, Mitten und Lichter sind natürlich entlang der X-Achse frei wählbar. In der Praxis wird man sich dabei natürlich eher daran orientieren, welche Bereiche tatsächlich von der Veränderung betroffen werden. Ein waschechter Color-Grader hat dabei jedoch immer folgende Bereiche vor dem geistigen Auge:
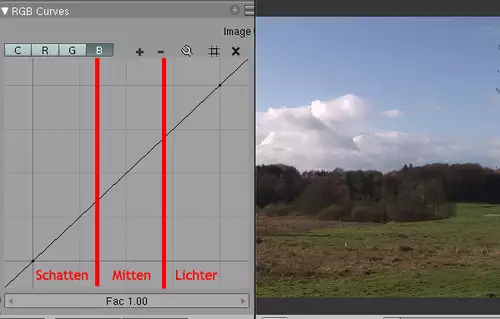
Angenommen, man will diesem Bild einen blaueren Himmel zugestehen (eher Lichter) und dabei aber nicht dem Rasen (eher Schatten) einen Blaustich verpassen. Im Gegenteil, vielleicht könnte der Rasen noch einen Tick gelber werden, um satter zu wirken. Kein Problem: folgende Kurve verstärkt bei Blau vor allem die Lichter und spendet dem Rest einen Tick Gelb, weil durch die Reduzierung von Blau nun Rot und Grün in den Schatten stärker dominieren. (Farbentheorie: Rot + Grün = Gelb).
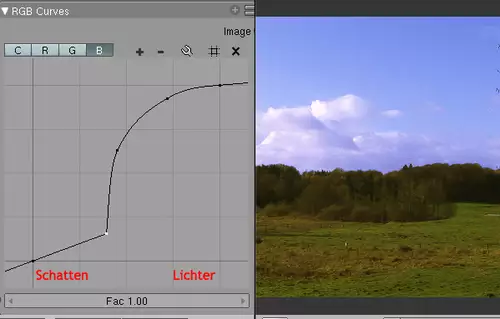
Sonst noch was?
Mit diesen Beispielen sind die Möglichkeiten der Gradationskurven natürlich bei weitem noch nicht ausgeschöpft. Ein einfacher Luma-Key ist beispielsweise durch eine invertierte Helligkeits-Kurve mit Schwellenwert zu erstellen...
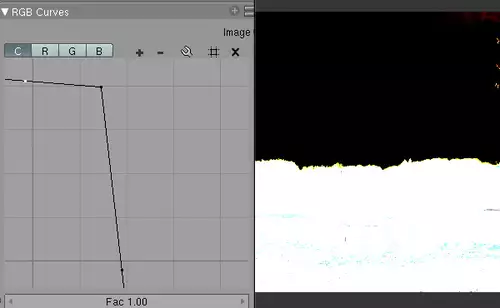
Aber Maskenbearbeitung und Effektkombinationen gehören nun wirklich in einen anderen Artikel. Schließlich sollten hier nur mal die Basics dargestellt werden. Bis zum nächsten Mal.